Kollokvium bringer i dag nytt om en meget stor begivenhet innen matematikken.
Enkelte matematiske problem forblir uløste over lang, lang tid. Selv om det kan være ganske lett å formulere problemet, kan det vært svært vanskelig å finne et bevis. Den japanske matematikeren Shinichi Mochizuki fra Kyoto har nemlig løst et matematisk problem som kalles “abc-formodningen”. Dette er like stort som å oppdage en ny elementærpartikkel innen fysikk.
En formodning er et matematisk resultat man tror er sant, men som ingen så langt har bevist. Enkelte slike formodninger blir stående uløst i lang, lang tid.
Ta for eksempel “Fermats siste sats”, som mange kanskje har hørt om: Pierre de Fermat var en stor fransk matematiker, dvs. egentlig var han advokat, men han syslet med matematikk på hobbybasis. Siden det var en hobby, brød han seg ikke så mye med å formulere beviser for arbeidet sitt til allmenheten. I 1637 formulerte han resultatet:
For heltall n > 2 finnes ingen positive heltallige løsninger av likningen an + bn = cn
Han skriblet i margen på en av arbeidsbøkene sine at “han hadde oppdaget et vidunderlig bevis, men det var for stort til å få plass i margen.”
350 år senere klarte matematiken Andres Wiles å bevise teoremet. Beviset var på 250 sider. Det tok åtte år i isolasjon.
Under arbeidet knyttet Wiles sammen vidt ulike matematiske grener, beviste svært viktige og fundamentale resultat innen et dusin felter innen alt fra grafteori, geometri og tallteori. Alt dette for å vise et enkelt utsagn som alle med ungdomsskolematematikk kan forstå.
For å si det mildt var dette et monumentalt arbeide og et stort gjennombrudd.
Den såkalte «abc-formodningen» er litt mer komplisert å beskrive enn Fermats siste teorem, og vi kommer tilbake til dette om litt. Formodningen ble fremsatt i 1985, og dersom den var sann, ville også en hel haug med viktige matematiske problem ha blitt løst, som ved et trylleslag! (Blant disse er faktisk Fermats siste teorem.) Et ganske gjevt problem å kunne løse, med andre ord.
Japaneren Mochizuki jobbet med dette problemet i lang tid, og tidligere i sommer begynte ryktene å svirre om at han hadde et bevis. Man sperret øynene opp og spisset ørene.
Beviset er offentliggjort. Det er på 500 sider, spredt over fire i seg selv imponerende artikler. (Klikk her for å se den første.)
Arbeidet er enormt. Mochizuki har funnet opp hele nye grener av matematikk under arbeidet, oppdaget mange nye matematiske konsepter, og det er nok ingen matematikere som forstår alt arbeidet hans. Det vil ta lang tid før resten av matematikkmiljøet har forstått alt sammen.
Mochizuki er heller ingen hvem-som-helst. Han begynte på universitetet 16 år gammel, og fikk doktorgrad 22 år gammel. Han er jevnt over beskrevet som et geni — ikke sånne vanlige genier som finnes her og der, men en person med en helt spinnvill og overmenneskelig matematisk kapasitet. Han jobbet som 17-åring med storheter som Ed Witten innen strengteori før han avanserte til ren matematikk, og er nå professor. Han har tidligere vist meget dype resultater.
Matematikermiljøet har med andre ord trua på dette.
Så hva er abc-formodningen?
Både Fermats siste teorem og abc-formodningen problemer innen tallteori. Dette er kanskje den mest grunnleggende disiplinen innen matematikk, og man studerer telletallene 1, 2, 3, osv. «Hva slags interessante problemstillinger finnes der?» kan man spørre. Vel, for det første kan all matematikk — i prinsppet — reduseres til tallteori. For det andre handler tallteori mye om primtall — tall som ikke er delelige med andre tall enn seg selv eller 1. (De første primtallene er 2, 3, 5, 7, 11, 13 og 17.) Primtall er svært viktige innen kryptografi.
abc-formodningen tar for seg likninger på formen a + b = c, derav navnet. Vi trenger også konseptet kvadratfrie tall. x er kvadratfri dersom x/n2 aldri går opp. 15 er ett eksempel, mens 12 ikke er det, siden 12/4 = 3, og 2∙2 = 4.
Ethvert tall kan faktoriseres i primtall. For eksempel 15 = 3∙5, 12 = 2∙2∙3. Den «kvadratfrie delen» sqp(x) til et tall x er det største tallet som kan konstrueres ved hjelp av primtallsfaktorene på en sånn måte at det er kvadratfritt. Puh! La oss ta 15. Den kvadratfrie delen av 15 er sqp(15) = 15 siden tallet er kvadratfritt i utgangspunktet. Hva med 12 = 2∙2∙3? Den kvadratfrie delen er sqp(12) = 6 = 2∙3.
Henger du med? Jeg vet at dette er litt komplisert, men vi er snart ved veis ende.
abc-formodningen sier nå:
La r være et tall større en 1. For enhver løsning av a + b = c, så vil sqp(a∙b∙c)r/c være større enn en konstant K som er større enn null.
La oss ta et eksempel (dette blir litt komplisert): Vi velger r = 2. La a = 3 og b = 125, slik at c = 128. Da kan man rekne ut sqp(abc) = 30 samt sqp(abc)2/c = 900/128. Man finner for r = 2 at sqp(abc)r/c er nesten alltid større enn 1, og alltid større en null. (Å finne den nøyaktige verdien for K kan være svært vanskelig — men tallet K finnes! Her er K et sted mellom null og 1.)
Yikes! Og dette har Mochizuki altså bevist. Hvordan har han gjort dette? Si det.
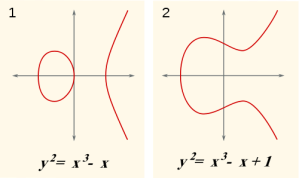
Det som sikkert kan sies er at I likhet med Andrew Wiles har han basert seg på teorien om elliptiske kurver. En elliptisk kurve er en graf som er beskrevet av likningen
og til høyre ser du et par eksempler. Som du ser likner dette litt på Fermats siste sats, og det med litt fantasi kan man godt se for seg hvordan arbeidet knytter sammen felter som geometri og tallteori. Men her stopper likheten med tidligere arbeid på abc-formodningen. Mochizuki har altså valgt sin helt egen angrepsvinkel på teorien om elliptiske kurver at andre matematikere nok må bruke flere år på å fordøye dette. Han kaller teorien «inter-universell Teichmüllerteori», og det er kjent at dette har videre anvendelser på andre problemer innen tallteori.
Arbeidet hans må nå gjennom en nøye granskning av et kobbel med ivrige matematikere. Det kan jo være at han tar feil! Innen matematikk er det alltid slik, at beviser må manuelt kontrolleres av uavhengige forskere for å finne ut om det er noen tabber der. Faktisk, når Andrew Wiles beviste Fermats siste teorem var det første beviset hans feil! Da han rettet det opp en stund senere hadde han utviklet enda mer banebrytende teori. Selv om Mochizuki har gjort noen feil på veien mot to streker under svaret er det rimelig sikkert at matematikken har gjort enorme fremskritt med publikasjonene hans.
Kilder: Nature, Wikipedia og Mochizukis hjemmeside.


«Matematikermiljøet har med andre ord trua på dette.»
Vel, selv om matematikere synes det er spennende med et potensielt bevis for ABC formodningen, merker jeg ikke kjempemye optimisme rundt Mochizukis arbeider ennå, heller mer forundring. Det holdes en rekke seminarer og forelesninger i disse dager for å sjekke detaliene i beviset, og det vil nok ta tid før folk godtar det som et fullverdig bevis. Men dette er virkelig et spesielt tilfelle: Som Brian Conrad ved Stanford sa nylig, er selv ekspertene innen feltet usikre på hva hovedideen i beviset går ut på.
Hei, og takk for kommentar!
Ja, utsagnet mitt er kanskje litt flåsete. Jeg har også oppfattelsen av at det er mye forundring snarere enn «yes endelig!» og kakeutdeling. Et veldig omfattende og komplekst arbeide som samtidig løser (påstås det) et svært viktig problem med meget obskure (har jeg inntrykk av) metoder gjør at det blir mye hodekløing blant matematikere som helst ikke vil uttale seg om felter de ikke jobber innen. Samtidig er det klart at Mochizuki er en velrenommert vitenskapsmann og dette gir grunn til optimisme. Det er nok liten tvil om at det er stor nyskapende tenkning bak, derfor de store ordene i denne populærvitenskapelige artikkelen.
Hei, jeg lurer på hva slags konsekvenser man ser av dette gjennombruddet f.eks i forhold til teknologi, dataprogramering osv. Hva kan man gjøre nå som man ikke kunne gjøre før dette gjennombruddet?
Hiver meg på denne. Og hvilke andre matematiske problemer kan en løse dersom dette beviset stemmer? Er det millennium-problemene?
Hei! Her er en liste over en del resultater som følger fra abc:
http://www.math.unicaen.fr/~nitaj/abc.html#Consequences
Ref til svaret mitt med lenke: Det er forresten ingen millennium-problemer blant disse så vidt jeg kan se.
Absolutt ingenting. Det kan hjelpe til å løse lignende matematiske problem, disse er gjerne av typen, «vi har sjekket at egenskap E holder for alle de første 50000 millioner tall, holder det for resten?».
Svært få direkte konsekvenser. Det finnes en del kryptografi som er basert på elliptiske kurver og deres relasjoner til primtall, men jeg har lest på mathoverflow.net at Mochizuki (visstnok) ikke gir eksplisitte resultater som kan brukes til å svekke kryptografiske algoritmer.
Det som er viktigere i denne sammenheng er alle resultatene som følger av abc-formodningen (se svar på annen kommentar). I tillegg kan man tenke seg hvordan ulike matematiske undergrener får et felles knutepunkt i abc, slik som Wiles arbeid med Fermats siste.
«For heltall n > 2 finnes ingen _positive_ heltallige løsninger av likningen a^n + b^n = c^n»
Hehe, ja du har jo rett i det … 🙂 Skal rette det opp!
Den norske matematikeren Sophus Lie utviklet teorier for elliptiske ligninger – som hadde betydning for bl.a. de matematiske formuleringer i relativitetsteorien. Har Lie’s arbeid vært av noen betydning for beviset av abc- formodningen (elliptiske kurver)?